lunes, 10 de junio de 2019

Parcial 3

  • ECUACIONES EXPONENCIALES Y LOGARÍTMICAS .
 ➥ FUNCIONES TRIGONOMÉTRICAS 

Algunas de las propiedades de una gráfica de las funciones trigonométricas son: dominio, máximo, asíntotas, periodo, alcance, etc.
Las funciones trigonométricas son: y=sen(x), y=cos(x), y=tan(x), y=cot(x), y=csc(x) o y=sec(x), en donde lo que está en el paréntesis es el dominio y “y” es el alcance.

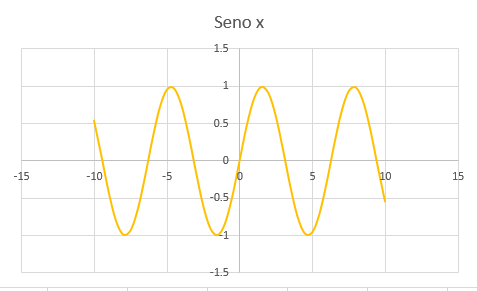
y = sen(x)


El ciclo de la función seno comienza en 0 y termina en 2π.
Dominio: el conjunto de números reales
Alcance: el conjunto de números mayores o iguales que -1 hasta los números menores o iguales que 1.
Cruza el eje de “y” en (0,0)
El eje de referencia es: eje “x”.
El punto máximo es:  (π/2,1)
El punto mínimo es: (3π/2,-1)
Su período: 2π.

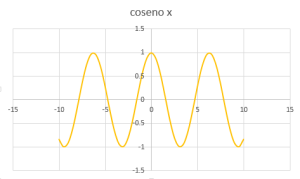
y = cos(x)

gráfica de las funciones trigonométricas 1















El ciclo fundamental de la función coseno del ángulo comienza en 0 y termina en 2π.
Dominio: el conjunto de números reales.
Alcance: el conjunto de números mayores o iguales que -1 hasta los números menores o iguales que 1.
Cruza el eje de “y” en: (0,1)
El eje de referencia es: el eje “x”
El punto máximo es:  (0,1) y (2π,1)
El punto mínimo es: (π,-1)
Su período: 2π

y = tan(x)

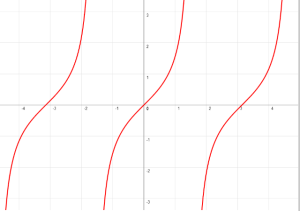
tangente

El ciclo fundamental de la función tangente del ángulo comienza en -π/2 y termina en π/2.
 Tiene asíntotas en el ciclo.
Dominio: toda x diferente a (π/2)±nπ
Alcance: el conjunto de todos los números reales.
Cruza el eje de “y” en  (0,0)
El eje de referencia es: el eje “x”
El punto máximo es:
El punto mínimo es:
Su período: π
Asíntotas: x=±π/2

 y = cot(x)

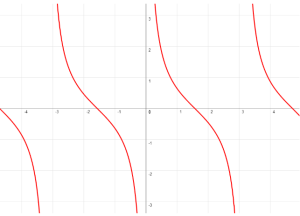
cotangente

El ciclo fundamental de la función cotangente del ángulo comienza en 0 y termina en π.
Tiene asíntotas en el ciclo.
Dominio: toda x diferente a ±nπ
Alcance: el conjunto de todos los números reales.
No cruza el eje de “y”
El eje de referencia es: el eje “x”.
Su período: π
asíntotas: x=±n

y = sec(x)


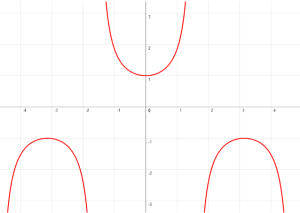
secante

El ciclo fundamental de la función secante del ángulo comienza en -π/2 y termina en 3π/2.
Tiene tres asíntotas verticales.
Dominio: el conjunto de números reales excepto los múltiplos impares de π/2
Alcance: el conjunto de todos los números reales menores menores o iguales que –1 y todos los números mayores o iguales que 1
Cruza el eje de “y” en (0,1)
El eje de referencia es: el eje “x”
El punto máximo es:  (π,-1)
El punto mínimo es:  (0, 1)
Su período: 2π
Asíntotas: x=-π/2, x=π/2 y x=3π/2

y = csc(x)

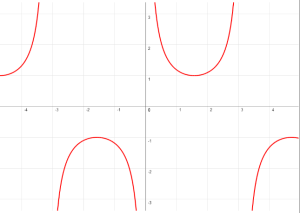
cosecante 


El ciclo fundamental de la función cosecante del ángulo comienza en 0 y termina en 2π.
Tiene tres asíntotas.
Dominio: el conjunto de números reales excepto los multiplos impares de π/2
Alcance: el conjunto de todos los números menores o iguales que -1 y todos los números mayores o iguales que 1
Cruza el eje de “y” en (0,1)
El eje de referencia es: el eje “x”
El punto máximo es:   (π,-1)
El punto mínimo es: (0, 1)
Su período: 2π
Asíntotas: x=-π/2, x=π/2 y x=3π/2

➧ EJERCICIOS 

PROBLEMAS POR RESOLVER:
*Hallar asíntota horizontal, asíntota vertical y puntos de corte de la siguiente función:


*Hallar asíntota horizontal, asíntota vertical y punto de corte de la siguiente función:

APROXIMACION IMFORMAL A LOS LIMITES:

PROBLEMAS POR RESOLVER:
*Hallar los puntos de límite de la siguiente función:
F (X)= 3X+6/X-1
*Hallar los puntos de límite de la siguiente función:
F (X)= X-5/2X-4         



FUNCION EXPONENCIAL:
FORMA GENERAL DE LA FUNCION EXPONENCIAL:


PROBLEMAS POR RESOLVER:
*Hallar la tabla de valores de la siguiente función:
F(X)= 2X/2X-3
*Hallar la tabla de valores de la siguiente función:
F(X)=2X-5/ X-3


⏭ Vídeos ⏮


https://www.youtube.com/watch?v=uMPx37LRI2E

https://www.youtube.com/watch?v=CRg5jQRj1Hg



Publicado por en No hay comentarios:

jueves, 4 de abril de 2019

FUNCIONES DE GRADO SUPERIOR


Parcial 1

Las funciones describen relaciones entre dos variables que intervienen entre diversos problemas o situaciones fenomenos del mundo real.
Las funciones se llaman asi porque generalmente su expresion algebraica es un polinomio, su forma general es:



 -Funcion polinomial La funcion de la funcion polinomial es:
Donde n es el numero real no negativo al igual que cada una de las constantes a, el grado del polinomio es a y su coeficiente de mayor grado osea an

 Propiedades: 1.la grafica de y=f(x) intercepta al eje y en punto 0,c
2. La grafica de y =f(x) intercepta al eje x en los puntos cuyas abcisas son las raices de la ecuacion a xn ++ a1x +a0 =0
3. Las funciones polinomiales son funciones continuas

 -Funcion constante
Es aquella que tiene la forma y=f(x)=c donde c es un numero real fijo El dominio de una funcion constante es R y su recorrido es {c} con una grafica en recta paralela al eje x

-Funcion Lineal Es aquella que tiene la forma o puede ser llevada a la forma y=f(x)=ax+b con a=0 abR


-Funcion cuadratica Tiene la forma o puede ser llevada a la forma Y=f(x)=ax2+bx+c, con a=0 ,abc y su dominio con R

- Funcion cubica Tiene la forma o puede ser llevada a la forma: Y=f(x)=ax3+bx2+cx+d con a=0 abcd y su dominio es R

Ceros de una funcion polinomial

Para hallar ceros de las funciones polinomiales de tercer o cuarto grado existen soluciones algebraicas sin embargo son muy complicadas y nada practicas Por lo cual se intentaran hallas los cero por tanteos pero siempre bajo un orden y utilizando un conjunto de herramientas y propiedades de los polinomios que nos permita proceder de una manera razonable y con presicion utilizando teorias cuyos numeros sean reales y racionales.


Teorema del Reciduo
Si un polinomio p(x) se divide entre x - a hasta obtener un residuo en el que no aparece la variable x el residuo resultante es igual a p(A)
Si dividimos p(x) entre x-a y designamos por Q (x) el cociente y por r el residuo entonces p(x) =Q(x)(x-a) +r Como la igualdad anterior es valida para todi xR lo sera para x=a luego





Teorema de factor
Si x=a es una raiz de ls ecuacion P(x)=0 donde p(x) es un polinomio entonces(xfa) es un factor de p(x)
Si (x-a) es un factor de p(x) implica que R=0 entonces tenemos p(x) =(x-a) Q(x) donde Q(x) es un polinomio como la igualdad es valida para todo numero real lo sera para x =a entonces x=a es una raiz de la ecuacion p(x)=0





Division sintetica
El teorema del residuo nos permite hallar el valor de un polinomio f(x) madiante la division de este entre un binomio pero hay una manera mas rapida de resolverlo que es mediante la division sintetica.



TRATAMIENTO VISUAL DE MÁXIMOS Y MÍNIMOS

La determinación de los valores máximos y mínimos de una función, es uno de los logros de la gran potencia que tiene el Cálculo. Tomemos f(x) como una función de x. El valor de x para el cual la derivada de f(x) con respecto a x es igual a cero, corresponden a los puntos de inflexión de la función f(x) donde sus valores son máximo y mínimo.

Resultado de imagen para tratamiento visual de maximos y minimos funciones de grado superior
Publicado por en 3 comentarios:

FUNCIÓN RACIONAL

Parcial 2 

  
Una función racional de una variable es una función que puede ser expresada de la forma:

Donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo, esta fracción es irreducible, es decir que las ecuaciones P(x) = 0 y Q(x) = 0 carecen de raíces comunes. Esta definición puede extenderse a un número finito pero arbitrario de variables, usando polinomios de varias variables. 

Modelo grafico: 



ASINTOTAS 

Se le llama asíntota de la gráfica de una función a una recta a la que se aproxima continuamente la gráfica de tal función.

Es decir la distancia entre las dos tiende a ser igual a 0, esto es a medida de que se extienden indefinidamente.

(Y= m·x+b) en coordenadas cartesianas.

Asíntotas verticales: rectas perpendiculares al eje de las abscisas, de ecuación x = constante. Asíntotas horizontales: rectas perpendiculares al eje de las ordenadas, de ecuación y = constante. Asíntotas oblicuas: si no son paralelas o perpendiculares a los ejes, de ecuación y = m•x + b.


EJEMPLOS : 









Publicado por en No hay comentarios:

FUNCIONES CUADRATICAS

La forma general de una función cuadrática es f ( x ) = ax 2 + bx + c . La gráfica de una función cuadrática es una parábola , un tipo de curva de 2 dimensiones

La parábola "básica", y = x 2 , se ve así:
.
EJEMPLO: 
Resuelve la siguiente ecuación cuadrática:
  \begin{equation*} x^2 - 4\,x + 1 = 0 \end{equation*}
por el método gráfico.
Empezamos graficando la función: y = x^2 - 4\,x + 1
Para graficar, empezamos calculando las coordenadas de los puntos a partir de unos valores de x:\\

Rendered by QuickLaTeX.com

como el vértice se encuentra en el punto (2,3), podemos escribir la ecuación de la forma:
  \begin{equation*} x^2 - 4\,x + 1 = (x-2)^2 - 3 = 0 \end{equation*}
Para verificarlo, puedes desarrollar el binomio al cuadrado.
¿Cómo obtuvimos este resultado? Usamos el método de factorización.
En este caso completamos el cuadrado perfecto:
  \begin{eqnarray*} x^2 - 4\,x + 1 &=& (x^2 - 4\,x + 1) + (4 - 4)\\ &=& (x^2 - 4\,x + 4) + (1 - 4)\\ &=& (x - 2)^2 - 3 \end{eqnarray*}
Observa que si x = 2, el binomio elevado al cuadrado tiene su mínimo valor: (x - 2)^2 = 0.
Y en ese caso, la gráfica pasa por el punto (2,-3). Este punto es el vértice de la parábola.
Para resolver la ecuación podemos utilizar el método de despeje:
  \begin{eqnarray*} (x - 2)^2 - 3 = 0\qquad&\Rightarrow&\qquad (x - 2)^2 = 3\\ x - 2 = \pm\sqrt{3}\qquad&\Rightarrow&\qquad x = 2\pm\sqrt{3} \end{eqnarray*}
Estas son las raíces que se muestran en la gráfica de la función que le corresponde a la ecuación.
Algunas veces, en geometría algunos problemas se resuelven a través de ecuaciones cuadráticas.




RAÍCES Y EL DISCRIMINANTE

formula cuadratica

El discriminante, precisamente es una parte de esta fórmula, pero una parte realmente muy importante ya que nos permitirá (si lo estudiamos por separado) determinar cuántas y qué tipo de soluciones tendrá la ecuación cuadrática en cuestión. De allí su nombre…, porque si lo piensas lo que nos permite en definitiva es discriminar.
discriminante ecuacion cuadrática

Se llama discriminante a la parte que está afectada por la raíz cuadrada, que, en la imagen anterior está destacada en color rojo.
casos dsicriminante


FORMAS, ESTÁNDAR Y FACTORIZADA 

Forma factorizada

    Toda función cuadrática se puede factorizar en función de sus raíces. Dada:
f(x) = ax^2 + bx + c \,
    se puede factorizar como:
f(x) = a(x - x_1)(x - x_2) \,
    siendo a el coeficiente principal de la función, por ello se extrae siempre como factor común, de no escribirse, el coeficiente de x2 sería siempre 1. x1 y x2 representan las raíces de f(x). En el caso de que el Discriminante Δ sea igual a 0 entonces x1 = x2 por lo que podríamos escribir:
f(x) = a(x - x_1)^2 \,
    En este caso a x1 se la denomina raíz doble, ya que su orden de multiplicidad es 2.

Forma estandar 



Publicado por en 1 comentario:
Suscribirse a: Entradas (Atom)