MATEMÁTICAS IV: FUNCIONES CUADRATICAS

La forma general de una función cuadrática es f ( x ) = ax 2 + bx + c . La gráfica de una función cuadrática es una parábola , un tipo de curva de 2 dimensiones

La parábola "básica", y = x 2 , se ve así:

.

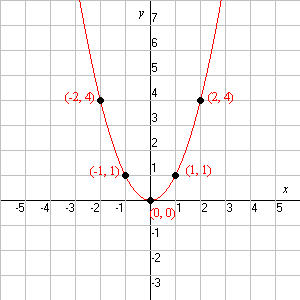EJEMPLO:

Resuelve la siguiente ecuación cuadrática:

$\begin{equation*} x^2 - 4\,x + 1 = 0 \end{equation*}$

por el método gráfico.

Empezamos graficando la función: $y = x^2 - 4\,x + 1$
Para graficar, empezamos calculando las coordenadas de los puntos a partir de unos valores de $x$ :\\

como el vértice se encuentra en el punto $(2,3)$ , podemos escribir la ecuación de la forma:

$\begin{equation*} x^2 - 4\,x + 1 = (x-2)^2 - 3 = 0 \end{equation*}$

Para verificarlo, puedes desarrollar el binomio al cuadrado.
¿Cómo obtuvimos este resultado? Usamos el método de factorización.
En este caso completamos el cuadrado perfecto:

$\begin{eqnarray*} x^2 - 4\,x + 1 &=& (x^2 - 4\,x + 1) + (4 - 4)\\ &=& (x^2 - 4\,x + 4) + (1 - 4)\\ &=& (x - 2)^2 - 3 \end{eqnarray*}$

Observa que si $x = 2$ , el binomio elevado al cuadrado tiene su mínimo valor: $(x - 2)^2 = 0$ .
Y en ese caso, la gráfica pasa por el punto $(2,-3)$ . Este punto es el vértice de la parábola.
Para resolver la ecuación podemos utilizar el método de despeje:

$\begin{eqnarray*} (x - 2)^2 - 3 = 0\qquad&\Rightarrow&\qquad (x - 2)^2 = 3\\ x - 2 = \pm\sqrt{3}\qquad&\Rightarrow&\qquad x = 2\pm\sqrt{3} \end{eqnarray*}$

Estas son las raíces que se muestran en la gráfica de la función que le corresponde a la ecuación.

Algunas veces, en geometría algunos problemas se resuelven a través de ecuaciones cuadráticas.

RAÍCES Y EL DISCRIMINANTE

El discriminante, precisamente es una parte de esta fórmula, pero una parte realmente muy importante ya que nos permitirá (si lo estudiamos por separado) determinar cuántas y qué tipo de soluciones tendrá la ecuación cuadrática en cuestión. De allí su nombre…, porque si lo piensas lo que nos permite en definitiva es discriminar.

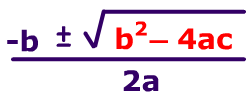
Se llama discriminante a la parte que está afectada por la raíz cuadrada, que, en la imagen anterior está destacada en color rojo.

FORMAS, ESTÁNDAR Y FACTORIZADA

Forma factorizada

Toda función cuadrática se puede factorizar en función de sus raíces. Dada:

$f(x) = ax^2 + bx + c \,$

se puede factorizar como:

$f(x) = a(x - x_1)(x - x_2) \,$

siendo a el coeficiente principal de la función, por ello se extrae siempre como factor común, de no escribirse, el coeficiente de x² sería siempre 1. x₁ y x₂ representan las raíces de f(x). En el caso de que el Discriminante Δ sea igual a 0 entonces x₁ = x₂ por lo que podríamos escribir:

$f(x) = a(x - x_1)^2 \,$